Beating the kCTF PoW with AVX512IFMA for $51k

Introduction

In May 2025, my Crusaders of Rust teammates William Liu (FizzBuzz101) and Savy Dicanosa (Syst3mFailure) discovered and developed an exploit of a use-after-free bug in Linux's packet scheduler. The bugfix patch contains additional details. William found this bug while fuzzing Linux for his master's thesis, which I will link here upon its publication. (Congratulations, William!)

They wanted to submit the bug to Google's kernelCTF competition for an anticipated $51,000 bounty.¹ Unfortunately, finding the bug and writing the exploit was only the first part of the battle. This post documents my small but unique contribution to our ultimately winning the bounty.

Setting the stage

To avoid paying out lots of money, kernelCTF organizers limit the number of submissions eligible for a bounty. Every two weeks at noon UTC, the submission window opens. Only the first team who is able to connect to and exploit the server, and submit the flag to a Google Form, receives a payout; any subsequent submissions are marked as duplicates. Furthermore, to prevent excessive submissions, the connecting to kernelCTF server requires solving a "proof of work"—a function which, by design, takes a few seconds to evaluate.

In summary, the submission process has these steps:

At 12:00:00 UTC, connect to the kernelCTF server.
Solve the proof of work, which takes roughly 4 seconds.
Wait for the instance to boot. (Roughly 2.5 seconds.)
Upload the exploit and run it to secure the flag. (Time elapsed depends on the exploit. Savy optimized this one to take roughly 0.55 seconds without sacrificing reliability. Wow!)
Submit the flag to a Google Form. The submission timestamp determines the winner of the "slot".

Our goal was to complete all these steps in sequence, faster than all the other teams.

Enter the sweats

Because of the large bounties, over time professional vulnerability research teams have aggressively optimized their submission process. For the May 2, 2025, submission window preceding ours, the first team to submit the flag did so 4.5 seconds after noon!

The numbers don't seem to add up: even assuming an instant exploit and form submission, the VM boot time and proof of work already take 6.5 seconds. Looking closer, we see that the time at which the winning submission's flag was generated (highlighted in red) is one second before noon UTC. Yet, the timestamp is generated after the proof of work is solved. Did sweaty CTFers invent time travel?

Alas! Because of a rounding quirk in the kernelCTF server code (here), the VM instance actually boots at 11:59:59—so no time travel. Still, the timestamp indicates that the winning team solved the proof of work in less than a second! How could this be?

We don't know for certain, but one kernelCTF organizer postulated that they were using field-programmable gate arrays (FPGAs). FPGAs are custom silicon that can perform specific tasks extremely quickly, to the exclusion of general-purpose tasks. They are not only fairly expensive, but also tricky to program. If the professional team had access to an FPGA programmed to perform the proof of work, a sub-second proof of work time was conceivable.

On May 13, William messaged me on Discord seeking advice on how to optimize the proof of work so that we could preempt the competition. I had to act fast: The next submission window would open at 5 a.m. PST, May 16.²

The proof of work: The "sloth" VDF

The proof of work (implemented here) is a certain verifiable delay function (VDF) known as "sloth". VDFs are cryptographic primitives which prove that a nontrivial amount of time has passed by requiring a long, serial computation. This computation outputs a proof which can be (relatively) quickly verified. Because the computation is serial, scaling to more computational resources (such as more CPU or GPU cores) does not reduce the runtime.³

The sloth VDF was introduced by Lenstra and Wesolowski (2015). I won't reproduce the number theory behind sloth (see page 4 of the paper for that), but to summarize matters, the function we must optimize boils down to:

def sloth_root(x, difficulty=7337):
    for i in range(difficulty):             # repeat the inner kernel this many times
        for j in range(1277):               # square x this many times
            x = (x * x) % (2 ** 1279 - 1)   # modulus is a Mersenne number
        x = x.bit_flip(0)                   # complement the LSB of x
    return int(x)

where x is a supplied 1280-bit integer. The difficulty variable linearly controls how long the VDF takes to solve.

Google's reference implementation uses gmpy, which is a Python binding to the venerable GNU Multiprecision Library (GMP). GMP's addition and multiplication kernels are handwritten in assembly for each target platform (example). The loop-carried dependency of x means that the computation is inherently serial, so throwing more cores at the problem—at least in a naïve way—is unhelpful. Meaningfully speeding up this function was going to be tough.

Initial progress

I set out on the obvious goal of optimizing the 1280-bit modular squaring (line 4 in the code above). The first success was mathematical: Because the modulus is a Mersenne number of length 1279 bits, and the intermediate product is 2 · 1280 = 2560 bits, computing the residue actually corresponds to a handful of cheaper operations:

def mod_2_1279_minus_1(x):    # compute x % (2 ** 1279 - 1)
    p = 2 ** 1279 - 1
    r = (x & p) + (x >> 1279)
    if r >= p:
        r -= p
    return r

I also translated the function to C++ to remove FFI overhead. The newly optimized code:

constexpr int MERSENNE_EXP = 1279;

mpz_t low, high, p;

void mpz_mod_mersenne(mpz_t r, const mpz_t x) {
    // p = 2^n - 1
    mpz_mod_2exp(low, x, MERSENNE_EXP);
    mpz_fdiv_q_2exp(high, x, MERSENNE_EXP);
    mpz_add(r, low, high);
    if (mpz_cmp(r, p) >= 0) {
        mpz_sub(r, r, p);
    }
}

bool init() {
    mpz_inits(low, high, p, NULL);
    mpz_ui_pow_ui(p, 2, MERSENNE_EXP);
    mpz_sub_ui(p, p, 1);
    return true;
}
bool _unused = init();

void the_powmod(mpz_t x) {
    for (int i = 0; i < 1277; ++i) {
        mpz_mul(x, x, x);
        mpz_mod_mersenne(x, x);
    }
}

int main()
{
    const int diff = 7337;
    mpz_t x, r;
    mpz_inits(x, r, NULL);
    mpz_set_str(x, "96729140485950483920373592475530255430", 10);
    for (int i = 0; i < diff; ++i) {
        the_powmod(x);
        mpz_combit(x, 0);
    }
    char *str = mpz_get_str(NULL, 10, x);
    std::cout << "x: " << str << std::endl;
    return 0;
}

This code ran in 1.9 seconds on my M1 Macbook Pro—a substantial improvement, and faster than similarly optimized solvers like this one written in Rust.⁴ William reported a further speedup by compiling libgmp locally with -march=native and linking it in statically—roughly 1.4 seconds on a fancy Intel Ice Lake laptop. Not bad, but still not a guaranteed win.

The modulus no longer being a bottleneck, I considered handwriting multiplication kernels in assembly to take advantage of the multiplication being a fixed width of 1280-bit × 1280-bit → 2560-bit; the factors fit neatly into twenty 64-bit limbs, and the product fits in forty limbs.⁵ GMP's assembly kernels are generic in the bitwidth, which introduces some overhead. Unfortunately, at 1.4 seconds we were approaching the theoretical limit of multiplication throughput, which is one 64-bit × 64-bit → 128-bit multiplication per cycle on all recent hardware.⁶

Enter AVX512

AVX512 is Intel's extension to the x86 ISA, first made available in 2016. It is a comprehensive overhaul of x86 SIMD programming, doubling the number and width of vector registers, adding Scalable Vector Extension–style mask predication, and hundreds of new instructions. It also has a troubled history: Linus Torvalds famously wished it to "die a horrible death", and despite supporting it on the Rocket Lake desktop CPUs, Intel disabled support for it starting with the Alder Lake µarch (2021); support continues in the server space. Meanwhile, AMD implemented AVX512 in their Zen 4 (2022) and Zen 5 µarches for both consumer and server CPUs.

Of present interest is the AVX512 Integer Fused Multiply–Add extension (AVX512IFMA), which was introduced specifically to speed up big-integer arithmetic—see, e.g., Ozturk, Kantecki & Yap (2024). I learned about AVX512IFMA during my competitive programming arc, optimizing submissions for judge.yosupo.jp. The extension introduces two new instructions which operate on vector registers:

vpmadd52luq – Packed Multiply of Unsigned 52-Bit Unsigned Integers and Add Low 52-Bit Products to 64-Bit Accumulators
vpmadd52huq – Packed Multiply of Unsigned 52-Bit Unsigned Integers and Add High 52-Bit Products to 64-Bit Accumulators

Essentially, the instructions perform the following operation (assuming the high 12 bits of each element in a and b are zero):

// vpmadd52luq dst, a, b
void vpmadd52luq(uint64_t dst[8], uint64_t a[8], uint64_t b[8]) {
    for (int i = 0; i < 8; ++i) {
        dst[i] += (a[i] * b[i]) & (1ULL << 52 - 1);
    }
}

// vpmadd52huq dst, a, b
void vpmadd52huq(uint64_t dst[8], uint64_t a[8], uint64_t b[8]) {
    for (int i = 0; i < 8; ++i) {
        dst[i] += ((__uint128_t)a[i] * b[i]) >> 52;
    }
}

In simpler terms, the instructions perform the low and high halves of a 52 × 52 → 104 multiplication, and accumulate the result into the destination register. At the execution unit level, the instructions reuse the multipliers used for double-precision floating point, and thus don't necessitate much extra silicon. They also have fantastic throughput: on Zen 5, which has a full 512-bit datapath, we can execute two of these instructions per clock!

At this point I was confident that I could make an extraordinarily fast VDF solver. All that was left was to implement it in two days....

The game plan

The natural radix for the AVX512IFMA extensions is 2⁵², i.e. 52-bit limbs stored in 64-bit words, so I let ChatGPT write a simple converter between GMP's representation and the 52-bit representation. We need ⌈1280 / 52⌉ = 25 limbs, which requires four 512-bit "zmm" registers (each register can store eight limbs, so the last register will only store one).

The first step is squaring the integer into a 50-limb intermediate product. We use a simple symmetry to almost halve the number of required multiplications, breaking up the desired value into two terms:

(a₂₄2^52·24 + a₂₃2^52·23 + ... + a₀)² = (a₂₄²2^52·48 + a₂₃²2^52·46 + ... + a₀²) + 2 i,j≤24∑i=0,j>ia_ia_j 2^{52·(i + j)}

Each of the yellow-highlighted multiplications produces a low term (furnished by vpmadd52luq) and a high term (furnished by vpmadd52huq).

Arranging the multiplications

First consider the second term above, the double summation highlighted in red. We want to reduce the number of shuffles necessary to get all the terms in the correct place, and use the "free" 64-bit accumulation as much as possible. One way to do this is to multiply a sliding window of 8 contiguous limbs by a single multiplier limb; all the output words, for both the low and high halves, will also be contiguous in the output. We can also use the merge masking feature to prevent accumulation of products that shouldn't be in the final sum, e.g., pairs where i = j. By selecting these windows and multipliers correctly, we can minimize the number of wasted multiplications.

// Computing the second term
// input contains the 25 52-bit limbs, stored in 64-bit words
_Alignas(64) uint64_t padded_data[8 * 6] = {0};  // so that loads OOB are still valid
uint64_t *data = padded_data + 8;

__m512i clumps[4] = {
    _mm512_loadu_si512(input),
    _mm512_loadu_si512(input + 8),
    _mm512_loadu_si512(input + 16),
    _mm512_loadu_si512(input + 24)
};

_mm512_store_si512(data, clumps[0]);
_mm512_store_si512(data + 8, clumps[1]);
_mm512_store_si512(data + 16, clumps[2]);
_mm512_store_si512(data + 24, clumps[3]);

#define ZERO _mm512_setzero_si512()

// Seven zmm accumulators are necessary
__m512i accum[7] = { ZERO /* 0-7 */, ZERO /* 8-15, etc. */, ZERO, ZERO, ZERO, ZERO, ZERO };
for (int i = -7; i <= 24; ++i) {
    // Sliding window
    __m512i m1 = _mm512_loadu_si512(data + i); // Load the current window of 8 elements
    for (int j = 0, k = 0; j < 7; ++j, k += 8) {
        // Decide whether to accumulate into accum[j], which should happen if there
        // is at least one element shared between the jth accumulator and [i, i+7]
        int lo = k - i;
        int hi = k - i - 1;
        // Process low halves
        if (lo >= 0 && lo <= 24) {
            // Discard out of bounds multiplications
            __mmask8 sel = (uint8_t)(lo < i ? -1ULL : (-1ULL << (lo - i + 1)));
            if (sel) {
                accum[j] = _mm512_mask_madd52lo_epu64(accum[j], sel, m1, _mm512_set1_epi64(data[lo]));
            }
        }
        // Process high halves
        if (hi >= 0 && hi <= 24) {
            // ditto
            __mmask8 sel = (uint8_t)(hi < i ? -1ULL : (-1ULL << (hi - i + 1)));
            if (sel) {
                accum[j] = _mm512_mask_madd52hi_epu64(accum[j], sel, m1, _mm512_set1_epi64(data[hi]));
            }
        }
    }
}

As an example, accumulator accum[1] contains output limbs 8 through 15, inclusive, and the following accumulations are executed (in this order):

Accumulating low halves: window 1 by limb 7 with mask 10000000
Accumulating high halves: window 1 by limb 6 with mask 11000000
Accumulating low halves: window 2 by limb 6 with mask 11100000
Accumulating high halves: window 2 by limb 5 with mask 11110000
Accumulating low halves: window 3 by limb 5 with mask 11111000
Accumulating high halves: window 3 by limb 4 with mask 11111100
Accumulating low halves: window 4 by limb 4 with mask 11111110
Accumulating high halves: window 4 by limb 3 with mask 11111111
Accumulating low halves: window 5 by limb 3 with mask 11111111
Accumulating high halves: window 5 by limb 2 with mask 11111111
Accumulating low halves: window 6 by limb 2 with mask 11111111
Accumulating high halves: window 6 by limb 1 with mask 11111111
Accumulating low halves: window 7 by limb 1 with mask 11111111
Accumulating high halves: window 7 by limb 0 with mask 11111111
Accumulating low halves: window 8 by limb 0 with mask 11111111

Here, window i contains limbs i through i+7 inclusive. Note that the masks mostly contain ones, indicating that we are not wasting too much multiplication throughput on masked-out elements.

Computing the first term is easier. We just square each element and interleave the low and high words:

for (int i = 0; i < 4; ++i) {
    __m512d diag_lo = _mm512_castsi512_pd(_mm512_madd52lo_epu64(ZERO, clumps[i], clumps[i]));
    __m512d diag_hi = _mm512_castsi512_pd(_mm512_madd52hi_epu64(ZERO, clumps[i], clumps[i]));
    __m512i shuf_lo = _mm512_set_epi64(11, 3, 10, 2, 9, 1, 8, 0);
    __m512i shuf_hi = _mm512_set_epi64(15, 7, 14, 6, 13, 5, 12, 4);
        accum[2 * i] = _mm512_add_epi64(accum[2*i], _mm512_castpd_si512(_mm512_permutex2var_pd(diag_lo, shuf_lo, diag_hi)));
    if (i != 3) {
        accum[2 * i + 1] = _mm512_add_epi64(accum[2*i+1], _mm512_castpd_si512(_mm512_permutex2var_pd(diag_lo, shuf_hi, diag_hi)));
    }
}

Finally, we need to implement the reduction modulo 2¹²⁷⁹-1. This is just a matter of selecting the upper 1279 bits and adding them to the lower 1279 bits. It's worth noting that at this point, the accumulator elements may exceed 2⁵²-1, but we can delay carry propagation until after the addition.

__m512i low_52_bits = _mm512_set1_epi64((1ULL << 52) - 1);
__m512i hi_12_bits = _mm512_set1_epi64(~((1ULL << 52) - 1));

__m512i high_1279[4];
shift_down_1279(accum, high_1279);
filter_low_1279(accum);

for (int i = 0; i < 4; ++i) {
    accum[i] = _mm512_add_epi64(accum[i], high_1279[i]);
}

{
carry2:;
__m512i carry_test = _mm512_setzero_si512();
__m512i group_out = _mm512_setzero_si512();
for (int i = 0; i < 4; ++i) {
    __m512i carries = _mm512_srli_epi64(accum[i], 52);
    __m512i carries_into = _mm512_alignr_epi64(carries, group_out, 7);
    accum[i] = _mm512_add_epi64(_mm512_and_si512(accum[i], low_52_bits), carries_into);
    group_out = carries;
    carry_test = _mm512_and_si512(carry_test, accum[i]); // improve latency over a series of masked tests
}

if (__builtin_expect(_mm512_test_epi64_mask(carry_test, hi_12_bits), 0)) {
    goto carry2;
}
}

We then need to subtract the Mersenne modulus if the addition is too large, but this is easy to check: we perform the subtraction iff the 1280th bit is 1. Subtracting 2¹²⁷⁹-1 is equivalent to subtracting 2¹²⁷⁹ (i.e., zeroing the 1280th bit) followed by adding 1 to the least-significant limb. Because the subtraction occurs with 50% probability, we do it in a branchless manner:

// Now compare with 2^1279 - 1; if >=, subtract 2^1279 - 1. classic Mersenne number modulo algorithm
__m512i bit_1279 = _mm512_set_epi64(0, 0, 0, 0, 0, 0, 0, 1ULL << 31);
__m512i mask_off = _mm512_set_epi64(0, 0, 0, 0, 0, 0, 0, (1ULL << 31) - 1);

// Branchless approach appears to save about 2 ns per iteration. Also, we stay in vector regs and don't use a test mask here because it tends to be slower
__m512i cmp = _mm512_and_epi64(accum[3], bit_1279);
accum[0] = _mm512_add_epi64(accum[0], _mm512_srli_epi64(cmp, 31));  // potentially +1 to last word
accum[3] = _mm512_and_si512(mask_off, accum[3]);

// TODO 1/2^52 chance of error here due to carry -- check it

There is a tiny chance that an overflow occurs in this last step: if the last limb happened to be exactly 2⁵²-1, then we'd need to propagate the carry. However, because PoWs are randomly generated, the probability this happens on any given run is about 2 in a billion—so I just ignored it.

At this point, the PoW was taking about 0.45 seconds on a rented Ryzen 9950X, which is a fast Zen 5 chip. Very promising!

Keeping the multiply–adds in flight

The multiply–add instructions have a latency of 4 cycles, and 2 can start every cycle. Thus, we need at least eight accumulators to fully saturate the multipliers instead of bottlenecking on latency, but we only have seven (and some of them are only used occasionally). The solution is to have fourteen accumulators—one set for the low halves and one set for the high halves—then merge them at the end:

__m512i accum[7] = { ZERO /* 0-7 */, ZERO /* 8-15, etc. */, ZERO, ZERO, ZERO, ZERO, ZERO };
__m512i accum_hi[7] = { ZERO, ZERO, ZERO, ZERO, ZERO, ZERO, ZERO };

// ... fmadd spam goes here ...

// Fold high and low halves
for (int i = 0; i < 7; ++i) {
    accum[i] = _mm512_add_epi64(accum[i], accum_hi[i]);
}

This brought the PoW down to roughly 0.32 seconds. The expanded AVX512 register file, with 32 zmm registers, came in clutch here.

Taming the register allocator

Inspecting the assembly revealed that both GCC and clang were unrolling the loop, converting the _mm512_set1_epi64 instructions into vbroadcastsd zmm, m64 instructions—one per limb—and then running out of vector registers during regalloc. Instead of rematerializing the values, they would stack-spill and reload the broadcasted vectors, causing considerable overhead.⁷

My solution was to use inline assembly to force the vpmadd52luq/vpmadd52huq instructions to use a memory broadcast operand for the multiplier limb. Instructions encoded with such an operand copy a single 32- or 64-bit element from memory to all elements of a vector operand, without consuming an architectural register. Moreover, this broadcast load does not consume any vector ALU resources: it is handled entirely by the load unit!

Now that we're using asm, the compiler can't remove masks of all 1s, so for optimal encoding we need separate asm for the all 1s case. Finally, when the multiplier limb happens to be at index zero in one of the zmm registers (i.e., multiples of 8), we use vpbroadcastq to splat it from register to register, which I measured to be a performance improvement over loading it from memory. The accumulation sequence is now:

if (lo >= 0 && lo <= 24) {
    // Multiples of 8 are handled by a register broadcast instead of a memory load for efficiency
#define FOR_EACH_OFFS X(1) X(2) X(3) X(4) X(5) X(6) X(7) X(9) X(10) X(11) X(12) X(13) X(14) X(15) X(17) X(18) X(19) X(20) X(21) X(22) X(23)
    __mmask8 sel = (uint8_t)(lo < i ? -1ULL : (-1ULL << (lo - i + 1)));
    if (sel == (uint8_t)-1 && ELIDE_MASKS_IF_POSSIBLE) {
#define X(n) case n: asm volatile ("vpmadd52luq %0, %1, %2%{1to8%}" : "+v"(accum[j]) :  "v"(m1), "m"(data[n])); break;
        switch (lo) {
            FOR_EACH_OFFS
            default:
            accum[j] = _mm512_madd52lo_epu64(accum[j], m1, _mm512_broadcast_i32x2(_mm512_castsi512_si128(clumps[lo/ 8])));
        }

    } else if (sel) {
#define X(n) case n: asm volatile ("vpmadd52luq %0 %{%1%}, %2, %3%{1to8%}" : "+v"(accum[j]) : "Yk"(sel), "v"(m1), "m"(data[n])); break;
        switch (lo) {
            FOR_EACH_OFFS
            default:
            accum[j] = _mm512_mask_madd52lo_epu64(accum[j], sel, m1, _mm512_broadcast_i32x2(_mm512_castsi512_si128(clumps[lo/8])));
        }
    }
}

(This is just for the low set of accumulators; the high set is nearly identical.) At this point, the PoW was taking roughly 0.23 seconds.

Creating the windows without touching memory

To compute the "windows", we are storing the integer to memory in an aligned fashion, then loading from it in an unaligned fashion. This is a classic situation that causes a store-forwarding stall, which further lengthens the critical path (the multiplications cannot commence until a window is loaded from memory). A better solution is to use the valignq instruction, which lets us simulate an unaligned load from the clumps array containing our integer.

__m512i m1;
if ((i & 7) == 0) {
    m1 = clumps[i / 8];
} else {
#define UNALIGNED(S) case S: { m1 = _mm512_alignr_epi64(clumps[(i+8)/8], i < 0 ? _mm512_setzero_si512() : clumps[(i+8)/8-1], S); break; }
    switch (i & 7) {
        UNALIGNED(1)
        UNALIGNED(2)
        UNALIGNED(3)
        UNALIGNED(4)
        UNALIGNED(5)
        UNALIGNED(6)
        UNALIGNED(7)
        default: abort();
    }
}

This brought the PoW down to 0.21 seconds. At this point, I decided to call it quits and sent my teammates the final C code.

May 16: Show time!

My friends got up at 4:30 a.m. PST, May 16, to prepare for the final submission; I couldn't be assed to be awake, so I slept until 6:30. They spun up a Zen 5 Google Cloud server in the Netherlands, geographically closest to the Google Form submission server, to minimize latency. A few minutes before 5:00, they recorded an intercepted POST request submitting the Google form, but with a dummy flag. The form submission program was devised and optimized by Bryce Casaje (strellic) and Larry Yuan (ehhthing). Max Cai also assisted in development and submission. Then at 5:00, the server connected to the kernelCTF server, solved the proof of work, ran Savy's optimized exploit, inserted the flag into the POST request, and sent it off....

We got it in 3.6 seconds—the fastest-ever kernelCTF submission! Later that day, the kernelCTF organizers confirmed our eligibility for the bounty and we all breathed a collective sigh of relief. Again, congratulations to Savy and William for discovering and exploiting this bug! Thanks to them for presenting me with the challenge, and thanks to my CSE 260 professor Bryan Chin (website) for what he taught us about program optimization.

The end of an era

On May 28, kernelCTF organizer koczkatamas announced that the proof of work was being removed:

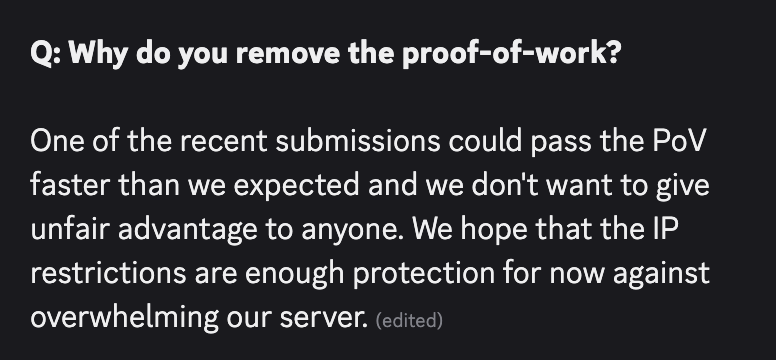
On the one hand, it's sad that we no longer have a competitive advantage, and the slot race becomes purely about exploit duration and network latency. On the other hand, at least people don't need to buy expensive FPGAs, or pull out their inline asm knowledge, to be on equal footing with the professionals. It also frees me to release this post!

Please message me on Discord (@forevermilk) if you have any comments or questions. I am also researching VDFs that are more resilient to assembly-level optimizations; if you have any ideas or would like to collaborate, I'm all ears.

I posted this to Hacker News and received some interesting commentary.

The final solver

This code is the product (ha!) of about 12 hours of work across May 14 and 15, and it is correspondingly unclean. Consider it released under the GNU AGPL 3.0.

// Written by Timothy Herchen
// gcc main.c -O3 -march=znver5 -masm=intel -lgmp
#include <immintrin.h>
#include <gmp.h>
#include <string.h>
#include <stdlib.h>
#include <stdio.h>
#include <stdint.h>
#include <stddef.h>

#define uint128_t __uint128_t

void gmp_to_array(mpz_t mpz, uint64_t *array) {
    size_t N;
    mpz_export(array, &N, 1, sizeof(uint64_t), 0, 0, mpz);
    for (int i = 0, j = N - 1; i < j; ++i, --j) {
	    uint64_t temp = array[i];
	    array[i] = array[j];
	    array[j] = temp;
    }
}

// Destroys the array
void array_to_gmp(uint64_t *array, mpz_t mpz, uint64_t words) {
    for (int i = 0, j = words - 1; i < j; ++i, --j) {
	    uint64_t temp = array[i];
	    array[i] = array[j];
	    array[j] = temp;
    }
    mpz_import(mpz, words, 1, sizeof(uint64_t), 0, 0, array);
}

size_t convert_radix_64_to_52(uint64_t *limbs, uint64_t *out, size_t count) {
    size_t out_index = 0;
    int bits_in_buffer = 0;
    uint128_t buffer = 0;

    for (size_t i = 0; i < count; i++) {
        buffer |= ((uint128_t)limbs[i]) << bits_in_buffer;
        bits_in_buffer += 64;

        while (bits_in_buffer >= 52) {
            out[out_index++] = (uint64_t)(buffer & ((1ULL << 52) - 1));
            buffer >>= 52;
            bits_in_buffer -= 52;
        }
    }

    // Handle remaining bits if any
    if (bits_in_buffer > 0) {
        out[out_index++] = (uint64_t)(buffer & ((1ULL << bits_in_buffer) - 1));
    }

    return out_index;
}

size_t convert_radix_52_to_64(uint64_t *in, uint64_t *out, size_t count) {
    size_t out_index = 0;
    int bits_in_buffer = 0;
    uint128_t buffer = 0;

    for (size_t i = 0; i < count; i++) {
        buffer |= ((uint128_t)in[i]) << bits_in_buffer;
        bits_in_buffer += 52;

        while (bits_in_buffer >= 64) {
            out[out_index++] = (uint64_t)(buffer & (((uint128_t)1ULL << 64) - 1));
            buffer >>= 64;
            bits_in_buffer -= 64;
        }
    }

    // Handle remaining bits if any
    if (bits_in_buffer > 0) {
        out[out_index++] = (uint64_t)(buffer & ((1ULL << bits_in_buffer) - 1));
    }

    return out_index;
}

__attribute__((always_inline)) void shift_down_1279(__m512i accum[7], __m512i high_1279[4]) {
	__m512i p = _mm512_setzero_si512();
#pragma GCC unroll 4
	for (int i = 3; i >= 0; --i) {
		__m512i down_31 = _mm512_srli_epi64(accum[i + 3], 31);
		__m512i higher_21 = _mm512_slli_epi64(_mm512_and_si512(accum[i + 3], _mm512_set1_epi64((1ULL << 31) - 1)), 21);
		high_1279[i] = _mm512_add_epi64(_mm512_alignr_epi64(p, higher_21, 1), down_31);
		p = higher_21;
	}
}

__attribute__((always_inline)) void filter_low_1279(__m512i accum[7]) {
	accum[3] = _mm512_and_si512(accum[3], _mm512_set_epi64(0, 0, 0, 0, 0, 0, 0, (1ULL << 31) - 1));
}

// This code is extremely latency bound, as you'd expect for this kind of stupid PoW, so certain things are done that would lower
// throughput (e.g. on a hyperthreaded device doing two of these at once) but which lower the latency
void the_powmod(uint64_t * __restrict__ input, uint64_t * __restrict__ result) {
	_Alignas(64) uint64_t padded_data[8 * 6] = {0};
	uint64_t *data = padded_data + 8;

	__m512i clumps[4] = {
		_mm512_loadu_si512(input),
		_mm512_loadu_si512(input + 8),
		_mm512_loadu_si512(input + 16),
		_mm512_loadu_si512(input + 24)
	};

	for (int pow_i = 0; pow_i < 1277; ++pow_i) {
		// Use aligned stores to make sure we are doing things well
		_mm512_store_si512(data, clumps[0]);
		_mm512_store_si512(data + 8, clumps[1]);
		_mm512_store_si512(data + 16, clumps[2]);
		_mm512_store_si512(data + 24, clumps[3]);

	// Now data[x] gives us the xth limb
#define ZERO _mm512_setzero_si512()

#define ELIDE_MASKS_IF_POSSIBLE 1

	__m512i accum[7] = { ZERO /* 0-7 */, ZERO /* 8-15, etc. */, ZERO, ZERO, ZERO, ZERO, ZERO };
	// The accumulation is latency bound (lat. 4 cycles, so we need at least 8 accumulators to keep the madds in flight)
	__m512i accum_hi[7] = { ZERO, ZERO, ZERO, ZERO, ZERO, ZERO, ZERO };
	// We'll laboriously build up the upper triangle of the 2560-bit product using 52x52->104 multiplies
#pragma GCC unroll 100
	for (int i = 24; i >= -7; --i) {
		// Sliding window
		__m512i m1;
		if ((i & 7) == 0) {
			m1 = clumps[i / 8];
		} else {
			// Emulate an unaligned load from memory. Unaligned loads are very expensive on Zen 5 so this is helpful
#define UNALIGNED(S) case S: { m1 = _mm512_alignr_epi64(clumps[(i+8)/8], i < 0 ? _mm512_setzero_si512() : clumps[(i+8)/8-1], S); break; }
			switch (i & 7) {
				UNALIGNED(1)
				UNALIGNED(2)
				UNALIGNED(3)
				UNALIGNED(4)
				UNALIGNED(5)
				UNALIGNED(6)
				UNALIGNED(7)
				default: abort();
			}
		}

#pragma GCC unroll 100
		for (int j = 0, k = 0; j < 7; ++j, k += 8) {
			// Decide whether to accumulate into accum[j], which should happen if there
			// is at least one element shared between the jth accumulator and [i, i+7]
			int lo = k - i;
			int hi = k - i - 1;
			if (lo >= 0 && lo <= 24) {
				// Multiples of 8 are handled by a broadcast instead of a memory load for efficiency
#define FOR_EACH_OFFS X(1) X(2) X(3) X(4) X(5) X(6) X(7) X(9) X(10) X(11) X(12) X(13) X(14) X(15) X(17) X(18) X(19) X(20) X(21) X(22) X(23)
				// Discard those entries where lo > i
				__mmask8 sel = (uint8_t)(lo < i ? -1ULL : (-1ULL << (lo - i + 1)));
				// we use inline asm with a memory broadcast after enough regs because the register allocator does not enjoy this type of setup
				if (sel == (uint8_t)-1 && ELIDE_MASKS_IF_POSSIBLE) {
#define X(n) case n: asm volatile ("vpmadd52luq %0, %1, %2%{1to8%}" : "+v"(accum[j]) :  "v"(m1), "m"(data[n])); break;
					switch (lo) {
						FOR_EACH_OFFS
						default:
						accum[j] = _mm512_madd52lo_epu64(accum[j], m1, _mm512_broadcast_i32x2(_mm512_castsi512_si128(clumps[lo/ 8])));
					}

				} else if (sel) {
#define X(n) case n: asm volatile ("vpmadd52luq %0 %{%1%}, %2, %3%{1to8%}" : "+v"(accum[j]) : "Yk"(sel), "v"(m1), "m"(data[n])); break;
					switch (lo) {
						FOR_EACH_OFFS
						default:
						accum[j] = _mm512_mask_madd52lo_epu64(accum[j], sel, m1, _mm512_broadcast_i32x2(_mm512_castsi512_si128(clumps[lo/8])));
					}
				}
			}

			if (hi >= 0 && hi <= 24) {
#undef X
				__mmask8 sel = (uint8_t)(hi < i ? -1ULL : (-1ULL << (hi - i + 1)));
				// see above
				if (sel == (uint8_t)-1 && ELIDE_MASKS_IF_POSSIBLE) {
#define X(n) case n: asm volatile ("vpmadd52huq %0, %1, %2%{1to8%}" : "+v"(accum_hi[j]) : "v"(m1), "m"(data[n])); break;
				switch (hi) {
					FOR_EACH_OFFS
					default:
					accum_hi[j] = _mm512_madd52hi_epu64(accum_hi[j], m1, _mm512_broadcast_i32x2(_mm512_castsi512_si128(clumps[hi / 8])) );
				}
				} else if (sel) {

#define X(n) case n: asm volatile ("vpmadd52huq %0 %{%1%}, %2, %3%{1to8%}" : "+v"(accum_hi[j]) : "Yk"(sel), "v"(m1), "m"(data[n])); break;
				switch (hi) {
					FOR_EACH_OFFS
					default:
					accum_hi[j] = _mm512_mask_madd52hi_epu64(accum_hi[j], sel, m1,_mm512_broadcast_i32x2(_mm512_castsi512_si128(clumps[hi / 8])));
				}
				}
			}

		}
	}

	// Fold high and low halves, and double all the accumulators
#pragma GCC unroll 7
	for (int i = 0; i < 7; ++i) {
		accum[i] = _mm512_add_epi64(accum[i], accum_hi[i]);
		accum[i] = _mm512_add_epi64(accum[i], accum[i]);
	}

	// Now add the diagonal from the accumulators because they weren't yet computed
#pragma GCC unroll 4
	for (int i = 0; i < 4; ++i) {
		__m512d diag_lo = _mm512_castsi512_pd(_mm512_madd52lo_epu64(ZERO, clumps[i], clumps[i]));
		__m512d diag_hi = _mm512_castsi512_pd(_mm512_madd52hi_epu64(ZERO, clumps[i], clumps[i]));
		__m512i shuf_lo = _mm512_set_epi64(11, 3, 10, 2, 9, 1, 8, 0);
		__m512i shuf_hi = _mm512_set_epi64(15, 7, 14, 6, 13, 5, 12, 4);
	        accum[2 * i] = _mm512_add_epi64(accum[2*i], _mm512_castpd_si512(_mm512_permutex2var_pd(diag_lo, shuf_lo, diag_hi)));
		if (i != 3) {
			accum[2 * i + 1] = _mm512_add_epi64(accum[2*i+1], _mm512_castpd_si512(_mm512_permutex2var_pd(diag_lo, shuf_hi, diag_hi)));
		}
	}

	// Now propagate carries in parallel in radix 2^52
	__m512i low_52_bits = _mm512_set1_epi64((1ULL << 52) - 1);
	__m512i hi_12_bits = _mm512_set1_epi64(~((1ULL << 52) - 1));

	// Now add the high 1279 bits to the low 1279 bits
	__m512i high_1279[4];
	shift_down_1279(accum, high_1279);
	filter_low_1279(accum);

#pragma GCC unroll 4
	for (int i = 0; i < 4; ++i) {
		accum[i] = _mm512_add_epi64(accum[i], high_1279[i]);
	}

	{
carry2:;
	__m512i carry_test = _mm512_setzero_si512();
	__m512i group_out = _mm512_setzero_si512();
#pragma GCC unroll 7
	for (int i = 0; i < 4; ++i) {
		__m512i carries = _mm512_srli_epi64(accum[i], 52);
		__m512i carries_into = _mm512_alignr_epi64(carries, group_out, 7);
		accum[i] = _mm512_add_epi64(_mm512_and_si512(accum[i], low_52_bits), carries_into);
		group_out = carries;
		carry_test = _mm512_and_si512(carry_test, accum[i]); // improve latency over a series of masked tests
	}

	if (__builtin_expect(_mm512_test_epi64_mask(carry_test, hi_12_bits), 0)) {
		goto carry2;
	}
	}

	// Now compare with 2^1279 - 1; if >=, subtract 2^1279 - 1. classic Mersenne number modulo algorithm
	__m512i bit_1279 = _mm512_set_epi64(0, 0, 0, 0, 0, 0, 0, 1ULL << 31);
	__m512i mask_off = _mm512_set_epi64(0, 0, 0, 0, 0, 0, 0, (1ULL << 31) - 1);

	// Branchless approach appears to save about 2 ns per iteration. Also, we stay in vector regs and don't use a test mask here because it tends to be slower
	__m512i cmp = _mm512_and_epi64(accum[3], bit_1279);
	accum[0] = _mm512_add_epi64(accum[0], _mm512_srli_epi64(cmp, 31));  // potentially +1 to last word
	accum[3] = _mm512_and_si512(mask_off, accum[3]);

	// TODO 1/2^52 chance of error here due to carry -- check it

#pragma GCC unroll 4
	for (int i = 0; i < 4; ++i) {
		clumps[i] = accum[i];
	}
	}

	_mm512_storeu_si512(result, clumps[0]);
	_mm512_storeu_si512(result + 8, clumps[1]);
	_mm512_storeu_si512(result + 16, clumps[2]);
	_mm512_storeu_si512(result + 24, clumps[3]);
}

int main(int argc, char **argv) {
	if (argc < 3) {
		fprintf(stderr, "Usage: %s <y> <difficulty>", argv[0]);
		return 1;
	}

	mpz_t x, r;
	mpz_inits(x, r, NULL);
	mpz_set_str(x, argv[1], 10);
	int difficulty = atoi(argv[2]);

	uint64_t abc[400];
	_Alignas(64) uint64_t poop[32];

	gmp_to_array(x, abc);

	size_t N = convert_radix_64_to_52(abc, poop, 20);

	uint64_t squared[1000];
	for (int i = 0; i < difficulty; ++i) { // specified algorithm
		the_powmod(poop, squared);
		squared[0] ^= 1;
		memcpy(poop, squared, 25 * sizeof(uint64_t));
	}
	convert_radix_52_to_64(squared, abc, 48);
	array_to_gmp(abc, r, 1280/64);

	char *str = mpz_get_str(NULL, 10, r);
	printf("%s", str);
	return 0;
}

I hope you enjoyed my first-ever blog post. Hopefully there will be many more.

Footnotes

$21,337 base reward, $10,000 for stability (successful exploitation on >90% of runs), and $20,000 for a 0-day bug. ↩
We had one shot at this; William's thesis was due in a few days and we wanted to include the exploit. ↩
Compare with proofs of work, for example, that request a SHA hash starting with some number of zeros. This process is embarrassingly parallel, so someone with many powerful GPUs could solve it in a fraction of the time as someone without. ↩
The Rust implementation uses the exact same Mersenne trick, yet takes about 2.4 seconds; I assume this is FFI overhead? 🤷 ↩
Limbs are the term of art for the integer elements of an array that represents a big integer. On 64-bit systems, limbs are usually 64-bit unsigned integers. ↩
See uops.info, imul r64 and mulx r64, r64, r64. ↩
The same performance problem was observed by y-cruncher author Alexander Yee here, section "Example 2: Everything Blows Up". ↩